Chapter 1 – System Architecture
Frequency mask and periodogram
Output perceptron with hysteresis
System
architecture can be explained by the following scheme:
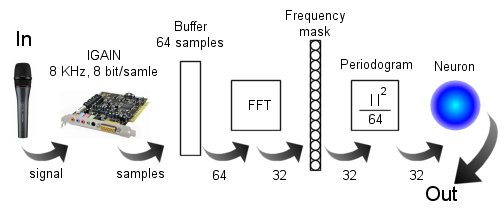
The
signal is read from the internal PC’s microphone, pre-amplified according to
SoundBlaster's input gain (IGAIN), sampled by the SoundBlaster’s DSP and
saved into a 64-samples buffer.
A
sampling frequency of 8 KHz and a sample size of 8 bit/sample turned out to be
suitable for the job.
Then,
signal is analysed in the frequencies through the periodogram, given by:
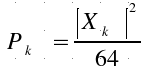, where 
, with k=1,...,32 and n=1,...,64.
A
frequency mask has been introduced to save time stopping the calculation for
periodogram’s samples whose frequencies are far from whistle’s ones.
Finally, periodogram samples at frequencies of interest become the input of a
perceptron, which detects the whistle. The perceptron’s activation function
is not a simple sgn(x) function, but hysteresis has been introduced, to avoid
spurious commutations in transient situations.
WR
simply accesses the SoundBlaster through “/dev/dsp”.
The
device is opened at startup, its parameters are immediately set (sampling
frequency, sample size, size and number of fragments for real-time).
After
these operations have been completed, WR starts reading blocks
of 64 samples continuously.
Before
shutting down, WR closes “/dev/dsp”.
[See
code: Audio.h]
[See
code: Audio.cpp]
This
is the slowest process of the job, so many adjustments have been made to make
it faster, by reducing the number of floating-point multiplications which need
to be done .
Starting
from the DFT formula:
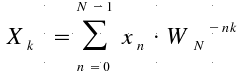
where:
is the time index
is the frequency index
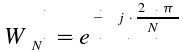
standard
fft (applyable when N is a power of 2)
proceeds subdividing the original sequence in 2 sub-sequences:
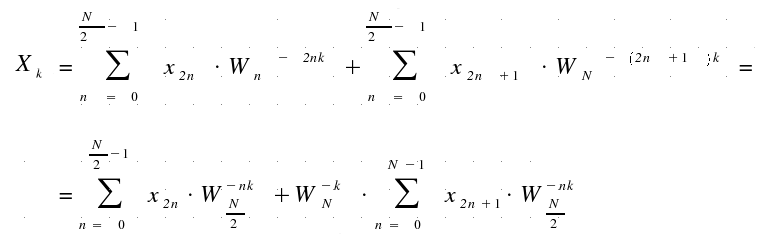
since this formula is valid for 0 <= k <=
N/2 – 1, a second formula is needed for the second half of the sequence:
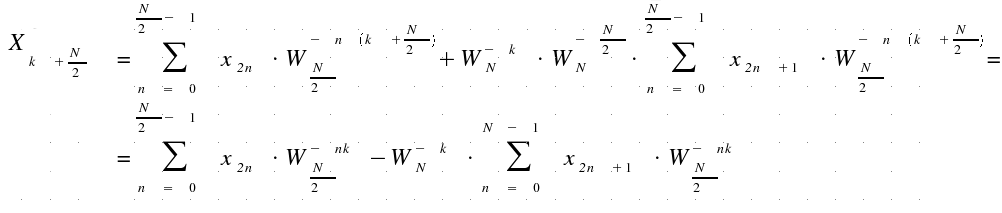
called:
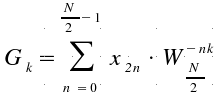
and
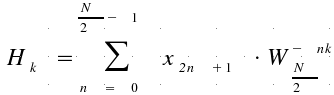
we
have:
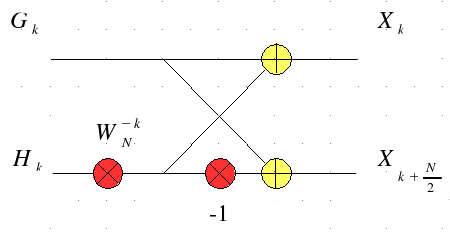
This scheme is called BUTTERFLY and is usually explained simply by drawing this scheme:
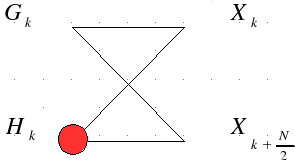
A
butterfly contains one complex multiplication (Hk
*
WN-k),
indicated with the red point.
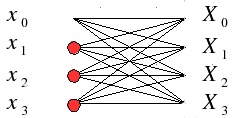
For istance, we have to do the following process to calculate the DFT of a 4-samples sequence:
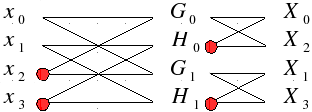
So,
4 butterflies must be calculated. Therefore, 4 complex multiplications are
needed to complete the job.
But
the original sequence can be subdivided in a number m of sub-sequences
different from 2 (3,4,5, etc.); obviously N must be a power of m.
A particular case is m = 4:
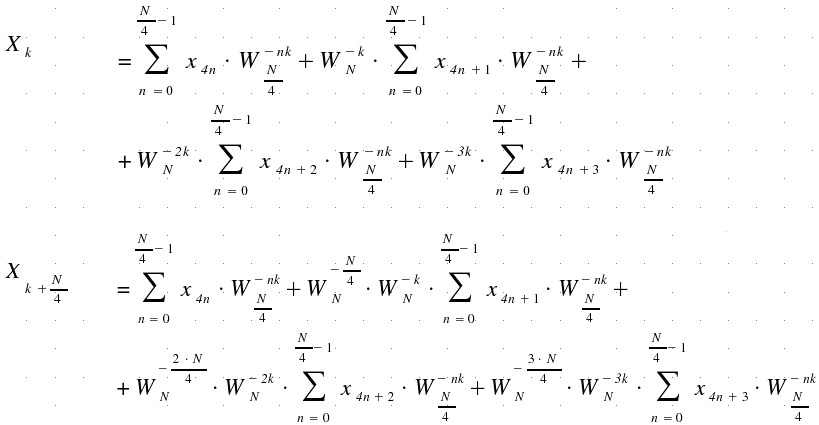
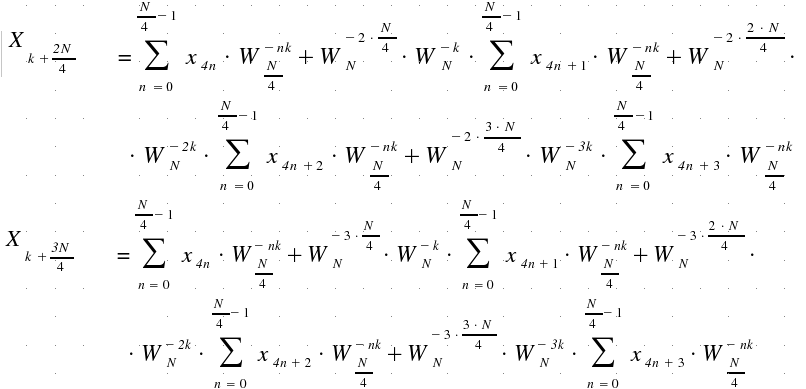
Calling:
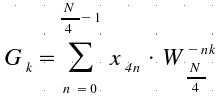
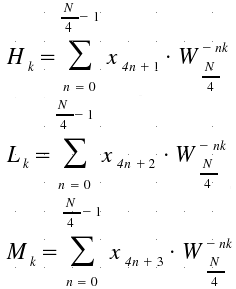
We
have the following situation:
which can be summarized with:
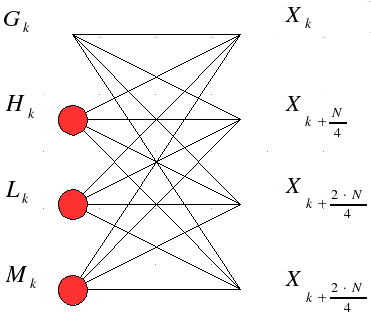
this
butterfly requires 3 complex multiplications: WN
matrix can be calculated without any multiplication.
Applying
this butterfly to a 4-samples sequence yields:
GK
= {xO},
HK
= {x1},
LK
= {x2},
MK
= {x3}
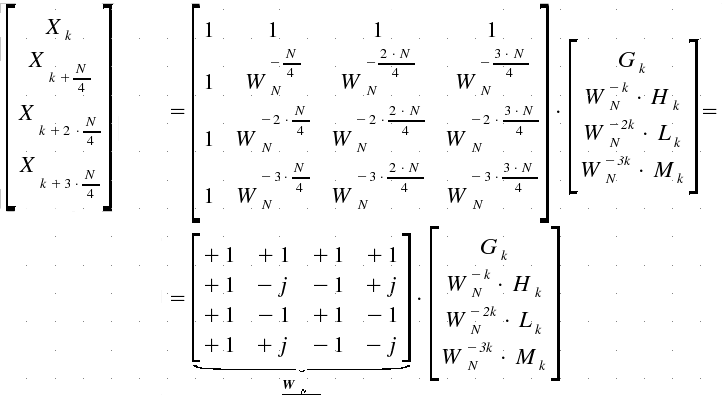
and:
Only
one butterfly is needed; so we complete the job with 3 complex multiplications,
while 4 multiplications were used with the standard butterfly.
Therefore,
using 4 sub-sequences will result in a (theorical) 25% gain in working time.
This
method is fully supported in WR, as it operates on 64-samples sequences, were
64 = 43.
Now,
symmetry property of DFT can be used to save even more time.
Actually
WR operates on real sequences (sampled audio), and the following property is
verified:
and
But
two real-sequence DFTs can be obtained from a single DFT of a complex sequence,
which is built as follows:
,
where
xn
and yn
are real sequences of the same length.
Transforming
sn
we have:
But:
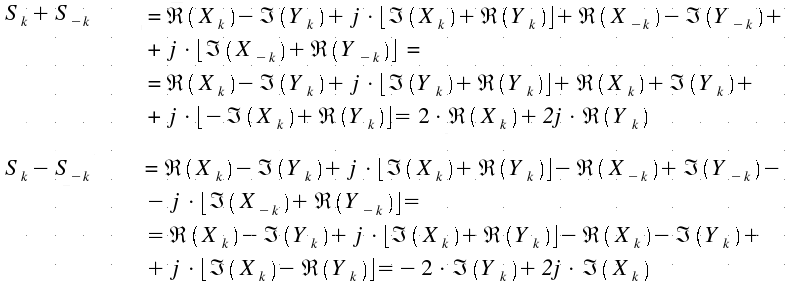
So XK and YK can be rebuilt with the following formulas:
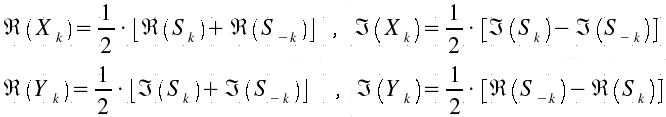
By doing this way, we
obtain a (theorical) 50% of gain in work time.
[See
code: Bars.h]
[See
code: Bars.cpp]
Some
periodogram's samples are far from the whistle's frequency and a recognition
based on those samples will result in a low-quality one. Therefore, the
correct frequencies must be selected. Correct frequencies are those that best
separate whistle samples from noise ones.
Data
separation is an index used to decide how much a periodogram's sample is good
separating whistle from noise. For each periodogram's sample, Data Separation
is calculated as follows:
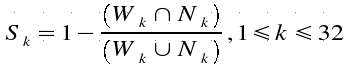
where
Wk and Nk are sets of values obtained from the k-th
periodogram's samples generated by 64-samples blocks of whistle or noise,
respectively.
Frequency
Mask and Periodogram
Not
every periodogram samples are to be considered for the recognition, and only
selected samples must be passed as an input to the perceptron.
Frequency
mask is a simple blocking mechanism implemented with a 32-bit structure: each
bit of the structure determines whether corresponding sample is passed or not
to the perceptron.
If
a sample must be discharged, it shouldn't be calculated at all: for this
reason, frequency mask has been introduced before the periodogram (|·|2/64)
calculation.
More
multiplications could be avoided integrating frequency mask in the fft by
blocking discharged samples before being calculated.
This
mechanism is quite difficult and has not been implemented, as fft work time is
acceptable.
Finally,
interesting periodogram samples are calculated, while the other samples are
forced to 0.
[See
code: FreqMask.h]
The
frequency skew introduced by doppler effect can be easily estimated with an
analysis based on acoustic theory:
We
know that:
1)
If
source moves in air while the observer is still, the heard frequency is:
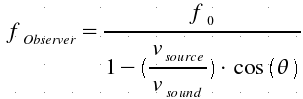
2)
If
the source is still and the observer moves in air, the heard frequency is:
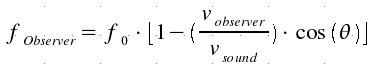
But
both the source (whistle) and the observer (robot) move in air; we can obtain
the correct formula considering two paths: from whistle to a still point P (using
formula 1) and from P to the robot (using formula 2).
In
this way it yields:
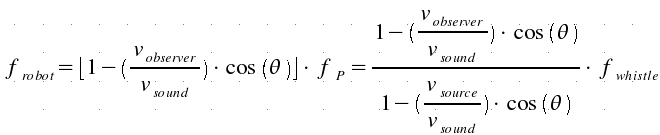
Sound
speed in air is experimentally set to 331.6 m/s at 0K, and it rises with the
square root of the temperature, in K.
At
room temperature, we have:
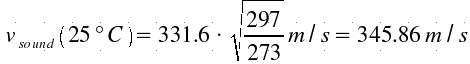
Assuming:
( a man running )
( robot speed )
( extimated from recorded samples )
the worst-case skew in frequency can be optained by:
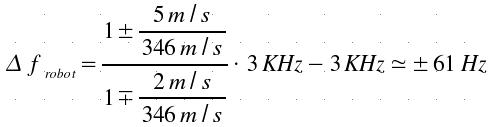
But
periodogram can be modelled with a bank of band-pass filters whose bandwitch
is
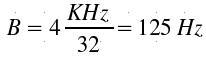
So,
frequency skew can be a 50% of period gram resolution and the whistle
frequency can be moved to the next or previous period gram sample by Doppler
effect.
For
this reason, perceptron uses a non-linear activation function and can extend
its frequency mask upon a sample forward or backward.
Output
perceptron with hysteresis
WR
uses a non-linear perceptron, in order to leave his behaviour unchanged even
if doppler effect shifts whistle's frequency.
If
a whistle rises sample i of the periodogram, Doppler effect can cause sample i
to remain low and sample (i+1) or (i-1) to rise instead.
This
suggests to use an activation function based on distance from origin, like a
sphere, instead of a simple plane.
WR
uses an ellipsoidal surface: if a point is internal to the surface, it would
be recognised as noise, otherwise it would be recognised as whistle.
The
introduction of hysteresis brings the division of the ellipsoid into two
ellipsoids that identify noise->whistle (turn-on) and whistle->noise
(turn-off) thresholds.
The
non-linear surface is described as follows:
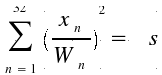, where x1...x32 are inputs and W1...W32
are perceptron's weights.
So,
the activation function (with hysteresis) is:
,
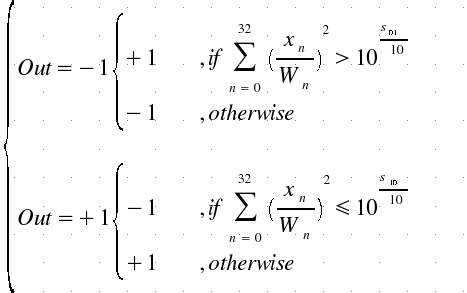where +1=Whistle and -1=Noise
Turn-on
and turn-off tresholds are defined in dB:
and 
The
perceptron's learning function always acts with turn-on and turn-off
thresholds that have been forced to 0 and finds a suitable weight vector.
Once
an optimal vector has been found, the user can introduce hysteresis.
Learning
rule for this perceptron is the following:
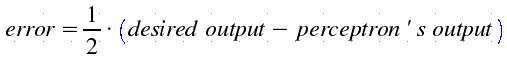
, where 
is the learning rate.
Actually,
if error is -1 , it means that perceptron outputted +1 (whistle) when it
should output -1 (Noise).
So,
a noise point, which must be internal to the ellipsoid, resulted external.
Since
Wk is the ellipsoid's radius on k axis, this weight must be raised
to let the ellipsoid include the example.
Doing
the inverse reasoning, it is easy to understand that the weight should be
lowered if error = +1.
Combining
the two cases, we obtain the learning rule which was previously discussed,
where the weight is adjusted proportionally to the relative perceptron's input
in the same direction.
Values
of the learning rate from 0 to 0.1 have been chosen to slow down the learning
loop in order to let the user see the weight vector changing through a
graphical representation.
Learning
rate can be greater than 0.1, nevertheless values greater than 0.9 caused on
some example sets large oscillations, preventing the reaching of the optimal
weight vector.
[See
code: Perc.h]
[See
code: Perc.cpp]
The
whistle counter module is directly connected to the perceptron's output and it
implements a fast algorithm, which detects whistle's length and multiplicity.
Output
of this algorithm are:
Short whistle
Long whistle
Multiple whistle (double, triple, and so on...)
WR
requires the user to define a set of parameters to determine what kind of
whistle has been played.
In
particular:
–
Time
step:
It defines the period of the main WR's timer, in milliseconds.
–
Short
if <:
The maximum length of a short whistle.
–
Long
if >:
The minimum length of a long whistle.
–
Interval
<:
The maximum length of the interval between two whistles to consider
them part of a multiple whistle.
–
Whistle
minimum length: The minimum length of a valid whistle.
–
Noise
minimum length:
The minimum
length of a valid noise.
[See
file: TimeSpecStruct.h]
The
most important feature of the algorithm is speed.
For
this reason, the chosen algorithm only reads the current perceptron's output
and stores all the previous states through a very small stack (5 bytes).
Input
of the algorithm is the perceptron's state (+1=whistle, -1=noise).
Output
of the algorithm is the message type (short, long, double, triple, ...)
The
algorithm also containes an internal Reliability control, based on how many
times the stack must be corrected to transform received signal in an ideal
whistle's one.
A
particular case is that of a single whistle, which length is between the
maximum length of a short whistle and the minimum length of a long whistle;
when it happens, the closest solution (short or long) is taken, but
reliability is forced to 80%.
Heart
of the algorithm is the “Process” function.
Every
time it is called (by the main WR's timer) it:
–
stores
the previous input (whistle or noise)
–
compares
the current input with the previous one and updates the stack.
–
when
a whistle is terminated and a long interval follows it (long means that it is
greater than the one specified by the “Interval <” field), it sends a
message.
The
stack stpres a list of events: an event is a whistle(W) or a noise(N),
followed by its length, in time steps.
For
instance, a 150ms whistle will be translated in a “W-15” event, using a
10ms time step, or in a “W-6” event, using a 25ms timestep; the same rule
is valid for noise using “N” in spite of “W”.
Every
time the current input equals the previous one, the current event on the stack
increments its length; lengths greater than 127 steps will be clamped to 127.
When
the input changes, the current event is pushed in the stack and a new event is
created; obviously, the new event will be a “N” event if the current inout
is -1, or a “W” event otherwise.
Doing
this operation, the algorithm controls the validity of the current event,
before pushing it: if the event is not valid, it will not be pushed, but it
will be considered part of the previous event and its length will be added to
the previous event's one; in this case, the current event is popped from the
stack.
For
instance, the “W-3” events in fig. 4.1 are not valid, since their length
is smaller than the one defined in the “Minimum
whistle's length” field, so they are eliminated.
A
similar case can be seen in fig. 4.2, where the “N-1” event is eliminated.
Each
time an event is eliminated, reliability is reduced to signal that an error
occourred.
This
is the basic mechanism: the cost is small because the work can be done with a
few comparisons and increments.
But,
as the first event is forced to “infinite noise” (or “N-127”), a
triple whistle requires only a 7-wide stack (N W N W N W N), but if we want
the algorithm to recognise a series of 100 whistles, we will need a 201-wide
stack!
To
correct this problem, a variable multiplicity has been introducted (mNumWhistles),
and the stack is collapsed to consider only the last whistle.
Fig.
4.3 is a good example of this mechanism.
A
first whistle is stored in stack[1]; the second whistle grows in stack[3];
when the second interval begins and the algorithm knows that the “W” event
in stack[3] is a valid whistle, multiplicity (shown as nW in the table) is
incremented and the “W” event is copied in stack[1], freeing space for the
following whistles.
The
new interval grows in stack[2] and can be regularly popped into stack[1] if it
is an invalid noise.
After
a long interval (greater than that specified through the “Interval <”
field), the algorithm returns a non-zero value which represents the message to
be sent: if the multiplicity is 1, the length of the whistle is read in order
to determine wether to send the “Short Whistle” or the “Long Whistle”
message; if multiplicity is greater than 1, it will be directly returned.
Doing
this way, the return value will be “Short Whistle”, “Long Whistle”, or
the multiplicity of the whistle; so , 2 means a double whistle, 3 means a
triple whistle, and so on...
Following
tables are the output from WRTeacher, compiling the counter module in test
mode.
The
first field is the input from the perceptron, the part is a shot of the
current stack, nW is the current multiplicity, the last field is the current
reliability.
-1 --->
0: N-127 1:
?-??? 2: ?-???
3: ?-??? 4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 1
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 2
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 3
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.98
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.98
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.98
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-???
nW: 0 Reliability: 0.98
+1
---> 0: N-127
1: W- 1
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.98
+1
---> 0: N-127
1: W- 2
2: ?-??? 3:
?-??? 4: ?-??? nW: 0 Reliability: 0.98
+1
---> 0: N-127
1: W- 3
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.98
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-???
nW: 0 Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-???
nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-???
2: ?-??? 3:
?-??? 4: ?-???
nW: 0 Reliability:
0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-???
nW: 0 Reliability: 0.96
+1
---> 0: N-127
1: W- 1
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 2
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 3
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 4
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 5
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 6
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 7
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 8
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 9
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 0.96
+1
---> 0: N-127
1: W- 10 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.96
-1
---> 0: N-127
1: W- 10 2:
N- 1
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 2
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 3
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 4
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 5
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 6
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 7
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 8
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 9
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 10
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 11
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 12
3: ?-??? 4:
?-???
nW: 1 Reliability: 0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 13
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 14
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.96
-1 ---> 0:
N-127 1: W- 10 2: N- 15
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.96
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 1.00
Fig.1.1 two invalid whistles followed by a (valid) short
whistle
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 1
2: ?-??? 3:
?-??? 4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 2
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 3
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 4
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 5
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 6 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 7
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 8
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 9
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 11 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 12 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 13 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability: 1.00
+1
---> 0: N-127
1: W- 14 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 15 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 16 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability: 1.00
+1
---> 0: N-127
1: W- 17 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 18 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 19 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 20 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 21 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 22 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 23 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 24 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 25 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability: 1.00
+1
---> 0: N-127
1: W- 26 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 27 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 28 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 29 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 30 2:
?-??? 3: ?-???
4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 31 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 32 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 33 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 34 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 35 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 36 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 37 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 38 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 39 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
+1
---> 0: N-127
1: W- 40 2:
?-??? 3: ?-???
4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 41 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 41 2: N- 1
3: ?-??? 4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 43 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 44 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 45 2:
?-??? 3: ?-???
4: ?-??? nW: 0
Reliability: 0.98
+1
---> 0: N-127
1: W- 46 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 47 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 48 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 49 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127 1:
W- 50 2: ?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 51 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 52 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability: 0.98
+1
---> 0: N-127
1: W- 53 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 54 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 55 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability: 0.98
+1
---> 0: N-127
1: W- 56 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 57 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 58 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 59 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 60 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 61 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 62 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 63 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 64 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 65 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 66 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 67 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 68 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 69 2:
?-??? 3: ?-???
4: ?-???
nW: 0
Reliability: 0.98
+1
---> 0: N-127
1: W- 70 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 71 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 72 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 73 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 74 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 75 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 76 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
+1
---> 0: N-127
1: W- 77 2:
?-??? 3: ?-???
4: ?-???
nW: 0 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 1
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 2
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 3
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 4
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 5
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 6
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77
2: N- 7 3:
?-??? 4: ?-??? nW: 1
Reliability: 0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 8
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 9
3: ?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 10
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 11
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.98
-1 ---> 0:
N-127 1: W- 77
2: N- 12 3:
?-??? 4: ?-???
nW: 1 Reliability:
0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 13
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 14
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.98
-1 ---> 0:
N-127 1: W- 77 2: N- 15
3: ?-??? 4:
?-??? nW: 1
Reliability: 0.98
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 1.00
Fig.1.2 a valid long whistle with a small
imperfection
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 1
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 2
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 3
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 4
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 5
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 6
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
+1
---> 0: N-127
1: W- 7
2: ?-??? 3:
?-??? 4: ?-??? nW: 0
Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
1 3: ?-???
4: ?-???
nW: 1 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
2 3: ?-???
4: ?-???
nW: 1 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
3 3: ?-???
4: ?-???
nW: 1 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
4 3: ?-???
4: ?-???
nW: 1
Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
5 3: ?-???
4: ?-???
nW: 1 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
6 3: ?-???
4: ?-???
nW: 1 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
7 3: ?-???
4: ?-???
nW: 1 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
8 3: ?-???
4: ?-???
nW: 1 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N-
9 3: ?-???
4: ?-???
nW: 1 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
7 2: N- 10
3: ?-??? 4: ?-???
nW: 1 Reliability:
1.00
-1 ---> 0:
N-127 1: W-
7 2: N- 11
3: ?-??? 4: ?-???
nW: 1 Reliability:
1.00
-1 ---> 0:
N-127 1: W-
7 2: N- 12
3: ?-??? 4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 1
4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 2
4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 3
4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 4
4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 5
4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 6
4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 7 4:
?-???
nW: 1 Reliability: 1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 8
4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 9
4: ?-???
nW: 1 Reliability:
1.00
+1
---> 0: N-127
1: W- 7
2: N- 12 3:
W- 10 4: ?-??? nW: 1
Reliability: 1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 1
3: ?-??? 4: ?-???
nW: 2 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 10
2: N- 2 3:
?-??? 4: ?-??? nW: 2
Reliability: 1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 3
3: ?-??? 4: ?-???
nW: 2 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 4
3: ?-??? 4: ?-??? nW:
2 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 5
3: ?-??? 4: ?-???
nW: 2 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 6
3: ?-??? 4: ?-???
nW: 2 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 7
3: ?-??? 4: ?-???
nW: 2 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 8
3: ?-??? 4: ?-???
nW: 2 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 9
3: ?-??? 4: ?-???
nW: 2 Reliability:
1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 10
3: ?-??? 4:
?-??? nW: 2
Reliability: 1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 11
3: ?-??? 4:
?-??? nW: 2
Reliability: 1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 12
3: ?-??? 4:
?-??? nW: 2
Reliability: 1.00
-1 ---> 0:
N-127 1: W- 10 2: N- 13
3: ?-??? 4:
?-??? nW: 2
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 1
4: ?-??? nW: 2
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 2
4: ?-??? nW: 2
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 3
4: ?-??? nW: 2
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 4
4: ?-??? nW: 2
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 5
4: ?-??? nW: 2
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 6
4: ?-??? nW: 2
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 7
4: ?-??? nW: 2
Reliability: 1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 8
4: ?-??? nW:
2 Reliability:
1.00
+1
---> 0: N-127
1: W- 10 2:
N- 13 3: W- 9
4: ?-??? nW: 2
Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N-
1 3: ?-???
4: ?-???
nW: 3 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N-
2 3: ?-???
4: ?-???
nW: 3 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N-
3 3: ?-???
4: ?-???
nW: 3 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N-
4 3: ?-???
4: ?-???
nW: 3 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N-
5 3: ?-???
4: ?-???
nW: 3 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N-
6 3: ?-???
4: ?-???
nW: 3 Reliability: 1.00
-1 --->
0: N-127 1:
W- 9
2: N- 7
3: ?-??? 4:
?-??? nW: 3
Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N-
8 3: ?-???
4: ?-???
nW: 3 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N-
9 3: ?-???
4: ?-???
nW: 3 Reliability: 1.00
-1 ---> 0:
N-127 1: W-
9 2: N- 10
3: ?-??? 4: ?-???
nW: 3 Reliability:
1.00
-1 ---> 0:
N-127 1: W-
9 2: N- 11
3: ?-??? 4: ?-???
nW: 3 Reliability:
1.00
-1 ---> 0:
N-127 1: W-
9 2: N- 12
3: ?-??? 4: ?-???
nW: 3 Reliability:
1.00
-1 ---> 0:
N-127 1: W-
9 2: N- 13
3: ?-??? 4: ?-???
nW: 3 Reliability:
1.00
-1 ---> 0:
N-127 1: W-
9 2: N- 14
3: ?-??? 4: ?-???
nW: 3 Reliability:
1.00
-1 ---> 0:
N-127 1: W-
9 2: N- 15
3: ?-??? 4: ?-???
nW: 3 Reliability:
1.00
-1 ---> 0:
N-127 1: ?-??? 2: ?-???
3: ?-??? 4:
?-??? nW: 0 Reliability: 1.00
Fig.1.3 a triple whistle whithout imperfections
[See code: Counter.cpp]
[See code: Counter.h]